National Institute for Nanotechnology, 11421 Saskatchewan Dr., Edmonton, AB, T6G 2M9, Canada; Department of Mechanical Engineering, University of Alberta, Edmonton, AB, T6G 2G8, Canada
e-mail:andriy.kovalenko@nrc.ca
http://www.cein.ualberta.ca/research/kovalenko/

Title: Statistical-mechanical, 3D molecular theory of solvation for multiscale modeling in nanochemistry and biophysics

Abstract:
A genuine challenge of multiscale modeling is theoretical coupling of methods at different scales, so that “observables” at lower-level scales are analytically linked to “force fields” of more coarsegrained models at higher-level scales. Statistical mechanics itself is in a sense an example of such theoretical coupling between microscopic variables and thermodynamic, macroscopic properties. The statistical-mechanical, three-dimensional molecular theory of solvation (a.k.a. 3D-RISM-KH) predicts from the first principles the solvation structure and thermodynamics of nanochemical and biomolecular systems in solution.¹ Rather than operating with trajectories of individual molecules, it yields 3D correlation functions of species in the statistical ensemble by solving the integral equations of liquid state theory, and then analytically gives the solvation thermodynamics in terms of the correlation functions. The method properly accounts for chemical functionalities by representing both electrostatic and non-polar features of the solvation structure, such as hydrogen bonding, solvophobicity, salt bridges, structural solvent, associative and electrochemical effects. We coupled the 3D-RISM-KH theory with ab initio methods (Kohn-Sham DFT and CASSCF) in a self-consistent field description (including analytical gradients) of electronic structure, optimized geometry, chemical reactions and nanocatalysis in solution.^1,2 We implemented the KS-DFT/3DRISM-KH multiscale method in the ADF computational chemistry package and extensively validated the method against experimental data for solvation thermochemistry, conformational equilibria, and activation barriers for various nanosystems in different solvents³ and ionic liquids.⁴ We also coupled the 3D-RISM-KH theory contracting solvent degrees of freedom with MD simulation of biomolecules, and implemented the MD/3D-RISM-KH method in the Amber molecular dynamics package.⁵ This included a number of accelerating schemes with several cutoffs for the interaction potentials and correlation functions, an iterative guess for the 3D-RISM solutions, and extrapolating solvent-induced forces and applying them in large multi-time steps (up to 20 fs) to enable simulation of large biomolecules. The MD/3D-RISM-KH method allows one to study large biomolecular systems involving rare solvent events occurring on extremely long timescales (e.g. solvent molecules, ions, and ligands in pockets and inner spaces), as the solvent statistics is accounted for statistically-mechanically. It also replaces MM/PB(GB)SA postprocessing using empirical non-polar terms with statistical-mechanical, MM/3D-RISM-KH evaluation of the solvation thermodynamics.^5,6 It yields at once 3D maps of binding affinity without phenomenological approximations, and thus has significant potential for computer-aided drug design.⁷ This talk will exhibit the KS-DFT/3D-RISM-KH and MD/3D-RISM-KH multiscale methods and illustrate their application to various nanochemical and biomolecular systems.

References
¹ A. Kovalenko, Three-dimensional RISM theory for molecular liquids and solid-liquid interfaces, in: Molecular Theory of Solvation, F. Hirata (ed.). Series: Understanding Chemical Reactivity, vol.24, (Kluwer, Dordrecht, 2003) pp.169-275, (and references therein).
² S. Gusarov, T. Ziegler, A. Kovalenko, J. Phys. Chem. A 110, 6083 (2006).
³ D. Casanova, S. Gusarov, A. Kovalenko, T. Ziegler, J. Chem. Theory Comput. 3, 458 (2007).
⁴ M.Malvaldi, S.Bruzzone, C.Chiappe, S.Gusarov, A.Kovalenko, J.Phys.Chem.B 113, 3536 (2009).
⁵ T. Luchko, S. Gusarov, D. R. Roe, C. Simmerling, D. A. Case, J. Tuszynski, A. Kovalenko, J. Chem. Theory Comput., 6, 607 (2010).
⁶ N. Blinov, L. Dorosh, D. Wishart, A. Kovalenko, Biophys. J. 98, 282 (2010).
⁷ T. Imai, K. Oda, A. Kovalenko, F. Hirata, A. Kidera, J. Am., Chem. Soc. 131, 12430 (2009).

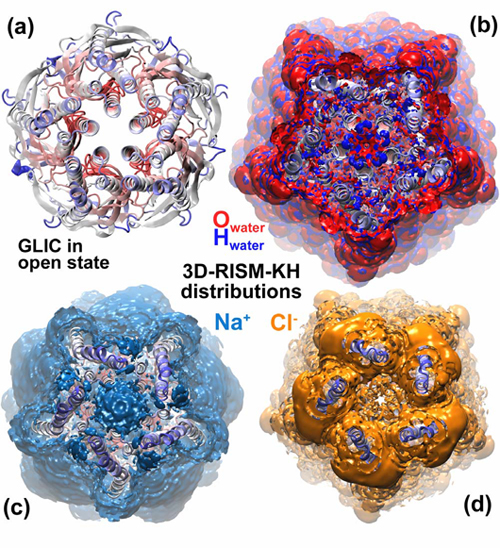
(a) Gloeobacter violaceus pentameric ligand-gated ion channel (GLIC) in an open state [Bocquet et al, Nature 457, 111 (2009)]. Top view at the ring of hydrophilic residues of GLIC M2 helices.
3D distributions of solvent in GLIC, obtained by the 3D-RISM-KH molecular theory of solvation:
(b) water O (in red) and H (in blue); (c) Na+ (in turquoise); (d) Cl- (in orange). Water forms a cap at the ring of hydrophilic residues, Na+ fill in the channel, and Cl- are depleted in the channel.